НАЗАД К СОДЕРЖАНИЮ

ЯМВЛИХ

ЖИЗНЬ ПИФАГОРА

---

Глава XXVI

Однажды он пребывал в напряженном размышлении над проблемой, можно ли придумать для слуха какой-нибудь вспомогательный инструмент, надежный и не вводящий в заблуждение, каким для глаза является циркуль, отвес и, разумеется, диоптры, а для осязания — весы и изобретение мер. По счастливой случайности проходя мимо кузницы, Пифагор услышал, как на наковальне ковали железо и одновременные удары молотов издавали очень гармоничные звуки, кроме одного сочетания. Он различил в них октаву и созвучия, построенные на квинте и кварте, а интервал между квартой и квинтой он видел как не образующий гармонии сам по себе, но заполняющий расстояние между ними.

116. Радуясь, как будто он получил эту идею от богов, он вбежал в кузницу и методом проб выяснил, что звучание зависит от тяжести молота, а не от силы удара, формы молота или изменения положения железа, которое ковали. Узнав точный вес молотов и установив, что их наклон при ударе одинаков, он удалился к себе домой. На один колышек, вбитый между углами стен (чтобы не внести в эксперимент никаких различных данных и чтобы вообще не было разницы между колышками), он повесил четыре струны из одного и того же материала, сплетенные из равного числа нитей, с одинаковой толщиной и одинаково скрученные. Он подвесил к ним разные грузы и сохранил равную их длину.

117. Затем, ударяя поочередно по паре струн, он нашел созвучия, о которых говорилось выше, в разных сочетаниях струн. Он установил, что струна, к которой прикреплен самый большой груз, и струна, к которой прикреплен наименьший груз, образуют октаву. Так как к первой было подвешено 12 гирек, а ко второй — шесть, то он открыл, что октаве свойственно отношение 2:1, что подтверждало и весовое соотношение гирек. С другой стороны, он открыл, что между струной с самым большим весом и ближайшей к самой легкой, имевшей восемь гирек, был интервал в квинту и, следовательно, полуторное отношение, и в полуторном отношении находились и подвешенные к ним грузы¹⁰⁴. Между струной с самым большим весом и следующей, которая была с большим грузом, чем другие, — к которой были подвешены девять гирек, — был интервал в кварту соответственно подвешенным грузам¹⁰⁵. Он выяснил, что эта струна (с девятью грузами) находится в отношении 3:4 к струне с самым большим грузом и что одновременно эта струна находится в полуторном отношении к струне с наименьшим весом,

118. поскольку девять именно так относится к шести¹⁰⁶. Равным образом струна, следующая за струной с наименьшим весом, к которой было прикреплено восемь гирек, образовывала со струной, имевшей шесть гирек, отношение 4:3, а со струной, которая имела 12 гирек, находилась в полуторном отношении. 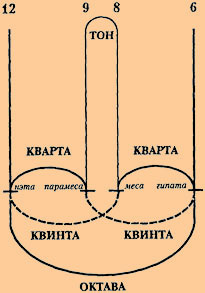Следовательно, интервал между квинтой и квартой, на который квинта превосходит кварту, был установлен в отношении 9:8¹⁰⁷. Звукоряд в октаве раскрывался двояко, либо с сочетанием квинты с квартой, как трехчленная пропорция 12:8:6¹⁰⁸, либо, в обратном порядке, с сочетанием кварты с квинтой, как трехчленная пропорция 12:9:6¹⁰⁹. Набив руку и изощрив слух на опытах с весами и открыв их пропорции, он искусно перенес общее крепление струн с вбитого на углу стены колышка на подставку под струны в лире, которую он назвал орудием натяжения струн, а натяжение струн в повороте колков в верхней части инструмента было аналогично подвешенным грузам.

119. Благодаря этому эксперименту, словно с помощью точного инструмента, он распространил наконец свой опыт на различные инструменты: цимбалы, флейты, свирели, монохорды, тригон¹¹⁰ и подобные им и нашел, что во всех них арифметическое отношение было одинаково гармоничным. Он назвал звук, соответствующий числу 6, гипатой¹¹¹, звук, соответствующий числу 8 и находящийся в отношении 4:3 к гипате, — месой¹¹², звук, следующий за месой, выражающийся числом 9 и звучащий тоном выше, чем меса, и находящийся к ней в отношении 9:8, — парамесой¹¹³, а звук, соответствующий числу 12, — нэтой¹¹⁴. Заполнив интервалы соответственно диатоническому роду пропорциональными звуками, он подчинил таким образом октахорд¹¹⁵ числовой гармонии, существующей в отношениях 2:1, 3:2, 4:3 и отличном от них отношении 9:8.

120. Таким образом он обнаружил в диатоническом роде необходимую и естественную прогрессию тонов от самого низкого звука к самому высокому. Начав с диатонического рода, он описал хроматический и энгармонический род, о чем мы расскажем, когда речь пойдет специально о музыке. Диатонический же род являет следующие ступени и такое естественное движение: полутон, тон, затем еще тон, и это есть кварта, соединение двух тонов и так называемого полутона. Затем, с прибавлением другого тона, вставленного в середину, образуется квинта, соединение трех тонов и полутона. Затем следуют полутон, тон и еще тон — другая кварта, то есть еще одно отношение 4:3. Поэтому в более древнем гептахорде¹¹⁶ каждый четвертый звук, начиная с самого низкого звука, образовывал созвучие кварты во всем звукоряде, причем полутон занимал поочередно первое, среднее и третье места тетрахорда. В пифагорейском октахорде,

121. представлял ли он сочетание тетрахорда с пентахордом или два несовпадающих тетрахорда, отделенные друг от друга целым тоном, мелодическое движение начиналось от самого низкого звука, так что каждый пятый звук образовывал созвучие квинты, а полутон здесь последовательно занимал четыре места: первое, второе, третье и четвертое. Вот так, рассказывают, открыл он искусство музыки и, изложив систематически, передал его ученикам для всех самых прекрасных целей.

к содержанию | примечания | к общему списку текстов